Flocking Gophers: The Boids Algorithm

tags: #go #golang

In 1987, Craig Reynolds published a paper describing his “Boids” algorithm for simulating the motion of “a flock of birds, a herd of land animals, or a school of fish”. A simple set of rules is applied to each animal (“boid”) individually:

“Each simulated bird is implemented as an independent actor that navigates according to its local perception of the dynamic environment”.

Nonetheless, from this local approach emerges an incredibly realistic, global flocking behaviour.

Emergent behaviour is absolutely fascinating to me - on hearing about this algorithm I had to implement it for a garrison of Gophers!

Complete source code can be found here. Special thanks to Conrad Parker for his excellent pseudocode breakdown of the Boids algorithm!

Graphics in Go

Before we dive into the nitty-gritty of the Boids algorithm, first we need a way of visualising our Gophers. This was a great opportunity to try out the excellent pixel 2D game library.

Creating a Window

With pixel, rendering the game window is pretty straightforward:

const (
	WorldWidth  = 1400
	WorldHeight = 800
	NumBoids    = 15
)

func createWindow(title string, width, height float64) (*pixelgl.Window, error) {
	window, err := pixelgl.NewWindow(pixelgl.WindowConfig{
		Title:  title,
		Bounds: pixel.R(0, 0, width, height),
		VSync:  true,
	})
	if err != nil {
		return nil, errors.Wrap(err, "new window failed")
	}
	window.SetSmooth(true)
	return window, nil
}

func Run() {
	window, err := createWindow("GoBoids", WorldWidth, WorldHeight)
	if err != nil {
		panic(errors.Wrap(err, "create window failed"))
    }
    // ...
}

func main() {
	pixelgl.Run(Run)
}

The Game Loop

The Run function can then be extended to implement the main game loop. This loop will be responsible for iteratively applying the game logic and redrawing the sprites on the window. Additionally, we use time.Tick to measure the frame rate of the game.

func Run() {
	window, err := createWindow("GoBoids", WorldWidth, WorldHeight)
	if err != nil {
		panic(errors.Wrap(err, "create window failed"))
	}
	strip, err := sprites.GophersStrip()
	if err != nil {
		panic(errors.Wrap(err, "get gophers strip failed"))
	}
	drawer := draw.NewDrawer(strip)
	world := boids.NewWorld(WorldWidth, WorldHeight, NumBoids)
	frames := 0
	second := time.Tick(time.Second)
	for !window.Closed() {
		err = drawer.DrawFrame(window, world)
		if err != nil {
			panic(errors.Wrap(err, "draw boids failed"))
		}
		world.Tick()
		window.Update()
		frames++
		select {
		case <-second:
			window.SetTitle(fmt.Sprintf("%s | FPS: %d", "GoBoids", frames))
			frames = 0
		default:
		}
	}
}

The key part here is in the loop, which repeatedly performs the following steps:

Redraw the internal representation of the game world on the window.
Update the game world.

Drawing Sprites

First we need some awesome Gopher pixel art - thanks to Egon Elbre!

Then we can create some logic for creating *pixel.Sprites from this sprite sheet. The full code can be found in /pkg/sprites, but the end result is that we can create a new Gopher SpriteStrip with:

strip, err := sprites.GophersStrip()

Then, to get a *pixel.Sprite for the particular Gopher at a given coordinate in the strip:

sprite, err := strip.NewSprite(pixel.Vec{
    X: 1,
    Y: 3,
})

Now we can use the (*pixel.Sprite) Draw method to render Gophers on the window!

The Boids Algorithm

Modelling the Game World

Now to define the internal representation of our Gophery game world. A World has some dimensions and a set of boids:

// World describes the boid universe.
type World struct {
	Width, Height int
	Boids         []*Boid
}

A Boid represents a single Gopher in the flock:


// Boid describes a single boid.
type Boid struct {
	ID                 int
	Alive              bool
	Position           pixel.Vec
    Velocity           pixel.Vec
    // Radius is the physical radius of the Boid on the screen
    Radius             float64
    // VisualRadius describes how far the Boid can see
    VisualRadius       float64
    // SeparationDistance is distance from its neighbours that a Boid likes to maintain
	SeparationDistance float64
	MaxSpeed           float64
}

Now, we can create a new World with randomly initialised Boids:

// NewWorld instatiates a new World with randomly initialised Boids.
func NewWorld(width, height int, n int) *World {
	boids := make([]*Boid, n)
	for i := 0; i < n; i++ {
		r := rand.Float64()
		maxSpeed := 8.0
		boids[i] = &Boid{
			ID:    i,
			Alive: true,
			Position: pixel.Vec{
				X: float64(rand.Intn(width)),
				Y: float64(rand.Intn(height)),
			},
			Velocity: pixel.Vec{
				X: r * maxSpeed,
				Y: (1 - r) * maxSpeed,
			},
			Radius:             25,
			VisualRadius:       100,
			MaxSpeed:           maxSpeed,
			SeparationDistance: 80.0,
		}
	}
	return &World{
		Width:     width,
		Height:    height,
		Boids:     boids,
	}
}

The Boids Algorithm

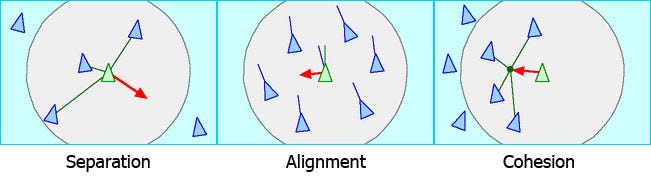
Boids Rules

Now the fun part: it’s time to implement the rules that produce emergent flocking behaviour. Reynolds' algorithm describes 3 essential rules that apply to each boid:

Cohesion
Separation
Alignment

The rules:

apply to each boid individually;
are functions of the positions & velocities of the boid’s neighbours; and
return a velocity vector that will be applied to the boid to adjust its position.

Each boid can only “see” its immediate neighbours, i.e. those that are within its VisualRadius. To get a boid’s neighbours:

// Neighbours returns the boids in the flock that are within the field of view of b.
func (b *Boid) Neighbours(flock []*Boid) []*Boid {
	var neighbours []*Boid
	for i := range flock {
		if !flock[i].Alive {
			continue
		}
		dist := math.Sqrt(
			math.Pow(flock[i].Position.X-b.Position.X, 2) + math.Pow(flock[i].Position.Y-b.Position.Y, 2),
		)
		if dist <= b.VisualRadius+flock[i].Radius {
			neighbours = append(neighbours, flock[i])
		}
	}
	return neighbours
}

These rules will be applied repeatedly to the boids with each “tick” of the game loop. We also include some extra rules to keep the boids on screen, as well as to limit their maximum speed (real-life Gophers can’t travel arbitrarily fast!):

// TickBoids updates the World's boids positions and velocities according to the rules.
func (w *World) TickBoids() {
	for i := range w.Boids {
		var vectors []pixel.Vec
		neighbours := w.Boids[i].Neighbours(w.Boids)
		vectors = append(vectors, w.Boids[i].Cohesion(neighbours, 0.001))
		vectors = append(vectors, w.Boids[i].Separation(neighbours, 0.005))
		vectors = append(vectors, w.Boids[i].Alignment(neighbours, 0.03))
		vectors = append(vectors, w.Boids[i].Bound(pixel.Vec{
			X: w.Boids[i].Radius,
			Y: w.Boids[i].Radius,
		}, pixel.Vec{
			X: float64(w.Width) - w.Boids[i].Radius,
			Y: float64(w.Height) - w.Boids[i].Radius,
		}))

		for _, vector := range vectors {
			w.Boids[i].Velocity = w.Boids[i].Velocity.Add(vector)
		}
		w.Boids[i].LimitVelocity(w.Boids[i].MaxSpeed)
		w.Boids[i].Position = w.Boids[i].Position.Add(w.Boids[i].Velocity)
	}
}

Cohesion

“Birds of a feather flock together”. This rule acts to encourage boids to fly together by steering the boid towards the average position of its neighbours:

// Cohesion steers the Boid to travel towards the center of the flock.
func (b *Boid) Cohesion(flock []*Boid, w float64) pixel.Vec {
	v := pixel.Vec{}
	if len(flock) == 0 {
		return v
	}
	for _, boid := range flock {
		if boid.ID != b.ID {
			v = v.Add(boid.Position)
		}
	}
	n := float64(len(flock) - 1)
	if n <= 0 {
		n = 1
	}
	return v.Scaled(1 / n).Sub(b.Position).Scaled(w)
}

Separation

Similarly, birds are smart enough not to fly into each other, and give each other enough room to manoeuvre. This rule steers the boid to maintain the desired SeparationDistance with its neighbours:

// Separation steers the the Boid to maintain the minimum separation distances with
// other Boids in the flock.
func (b *Boid) Separation(flock []*Boid, w float64) pixel.Vec {
	v := pixel.Vec{}
	if len(flock) == 0 {
		return v
	}
	for _, boid := range flock {
		if boid.ID != b.ID {
			if boid.Position.Sub(b.Position).Len() < b.SeparationDistance {
				v = v.Sub(boid.Position.Sub(b.Position))
			}
		}
	}
	return v.Scaled(w)
}

Alignment

Creatures in real-life flocks, herds and schools don’t just group together, but they also move in roughly the same direction as their neighbours. This rule steers the boid to align the direction in which it is moving with the other nearby boids:

// Alignment steers the Boid to align it's velocity direction with the
// other Boids in the flock.
func (b *Boid) Alignment(flock []*Boid, w float64) pixel.Vec {
	v := pixel.Vec{}
	if len(flock) == 0 {
		return v
	}
	for _, boid := range flock {
		if boid.ID != b.ID {
			v = v.Add(boid.Velocity)
		}
	}
	n := float64(len(flock) - 1)
	if n <= 0 {
		n = 1
	}
	return v.Scaled(1 / n).Sub(b.Velocity).Scaled(w)
}

Watch the Gophers Flock!

Now that we can update the positions of our Gophers according to the Reynolds' rules, the final step is to render them on screen! For this, we create a Drawer which will support batch rendering of sprites from a SpriteStrip:

// Drawer enables batch drawing sprites from a given strip.
type Drawer struct {
	Batch       *pixel.Batch
	SpriteStrip *sprites.Strip
}

// NewDrawer creates a new Drawer for the given sprite strip.
func NewDrawer(strip *sprites.Strip) *Drawer {
	return &Drawer{
		Batch:       pixel.NewBatch(&pixel.TrianglesData{}, strip.Asset),
		SpriteStrip: strip,
	}
}

Then with each frame we can batch draw the Gophers on the window at their given positions. Additionally we render a semi-transparent circle around the Gopher to indicate its visual radius:

// DrawFrame draws the world on the window.
func (d *Drawer) DrawFrame(window *pixelgl.Window, world *boids.World) error {
	window.Clear(colornames.Aliceblue)
	d.Batch.Clear()
	for i, boid := range world.Boids {
		if !boid.Alive {
			continue
		}
		gopher := sprites.Gophers["normal"]
		sprite, err := d.SpriteStrip.NewSprite(gopher)
		if err != nil {
			return errors.Wrap(err, "new gopher failed")
		}

		// Render visual radius of boid
		imd := imdraw.New(nil)
		imd.Color = color.RGBA{
			colornames.Blue.R,
			colornames.Blue.G,
			colornames.Blue.B,
			0x33,
		}
		if isPredator {
			imd.Color = color.RGBA{
				colornames.Red.R,
				colornames.Red.G,
				colornames.Red.B,
				0x33,
			}
		}
		imd.Push(boid.Position)
		imd.Circle(boid.VisualRadius, 0)
		imd.Draw(d.Batch)

		// Render boid itself as a Gopher
		theta := boid.Velocity.Angle()
		if theta < 0 {
			theta += 2 * math.Pi
		}
		sprite.Draw(
			d.Batch,
			pixel.IM.Moved(boid.Position).Scaled(
				boid.Position,
				// size boid according to radius, using the original size of sprite
				2*boid.Radius/float64(d.SpriteStrip.SpriteWidth),
			).Rotated(
				boid.Position,
				// gopher's head is upright so offset by -90deg to align head with x axis
				theta-(math.Pi/2),
			),
		)
	}
	d.Batch.Draw(window)
	return nil
}

Now we’ve got some flocking Gophers!

Gophers

Hunting Gophers

For a little extra fun, can we simulate hunting and evasion behaviour by adding an evil carnivorous predator to the mix?

This can be achieved with an additional Hunt rule that is applied to “predator” boids only. Similarly, AvoidLocation can be applied to the “prey” boids to simulate predator evasion tactics.

// Hunt returns a vector towards the nearest boid in the flock.
func (b *Boid) Hunt(flock []*Boid, w float64) pixel.Vec {
	v := pixel.Vec{}
	if len(flock) == 0 {
		return v
	}
	var target *Boid
	minDistance := math.MaxFloat64
	for i, boid := range flock {
		if boid.ID != b.ID {
			distance := math.Sqrt(
				math.Pow(boid.Position.X-b.Position.X, 2) - math.Pow(boid.Position.Y-b.Position.Y, 2),
			)
			if distance < minDistance {
				minDistance = distance
				target = flock[i]
			}
		}
	}
	if target == nil {
		return v
	}
	if minDistance < target.Radius {
		target.Alive = false
	}
	return b.TendToLocation(target.Position, w)
}

// TendToLocation returns a vector pointing towards the given location, weighted by w.
func (b *Boid) TendToLocation(vec pixel.Vec, w float64) pixel.Vec {
	return vec.Sub(b.Position).Scaled(w)
}

// AvoidLocation returns a vector pointing away from the given location, weighted by w.
func (b *Boid) AvoidLocation(vec pixel.Vec, w float64) pixel.Vec {
	return b.TendToLocation(vec, -w)
}

Predators

For full details, check out the source code! If you’ve got cool feature ideas, PR’s are welcome! You can also hit me up on Twitter ✌️